Electrons in few dimensions
- The integer quantum Hall effect (2D)
- The fractional quantum Hall effect (2D)
- One-dimensional electron transport (1D)
- Coulomb blockade in a quantum dot (0D)
The integer quantum Hall effect
At high magnetic field B, the electronic density of states becomes a set of discrete Landau levels due to the confinement produced by the field. The following diagram shows the Fermi circle in two dimensional k-space, with a series of Landau levels inside it.
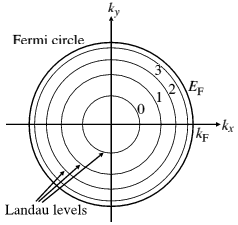Figure 1: Fermi circle in 2D.
When these levels are well resolved, if a voltage is applied between the ends of a sample, the voltage drop between voltage probes along the edge of a sample can go to zero in particular ranges of B, and the Hall resistance becomes extremely accurately quantised (the Quantum Hall Effect, QHE). The special values of field are those at which the ratio of the number of electrons per unit area to the number of units of flux h/e is an integer. This ratio is called the filling factor, and is denoted by the Greek letter nu.
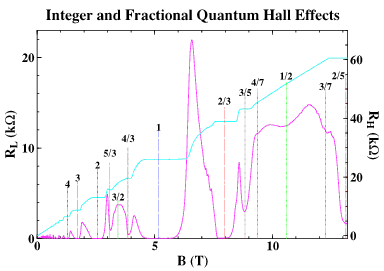Figure 2: Quantum Hall effect.
The QHE can be described in terms of a set of states, one per Landau level, travelling along the edges. The nature of these edge states is of great interest, and much work has been done to try to examine their structure and the way in which they modify the potential of the edge.
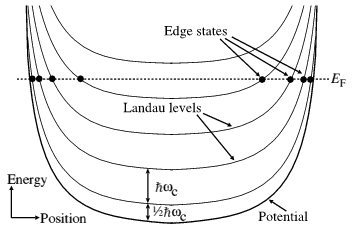Figure 3: Landau levels in real space.
In real space, taking a cross-section across the sample, the Landau levels follow the potential, rising up at the edges of the sample, as shown above. A typical "Hall bar" sample is sketched in Figure 4 below, showing, with crosses, the Ohmic contacts to source, drain and voltage probes. Edge states are indicated by lines with arrows.
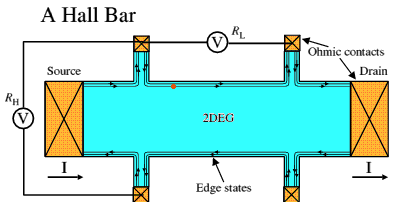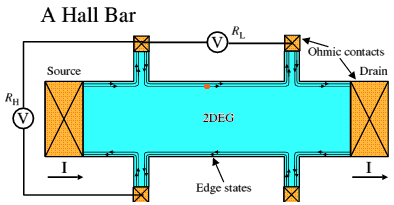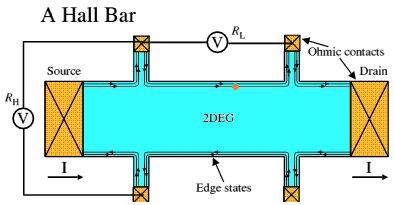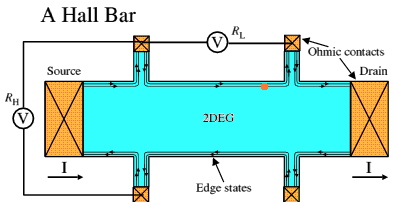Figure 4: Hall bar.
The fractional quantum Hall effect
The fractional quantum Hall effect (FQHE) is a fascinating manifestation of simple collective behaviour in a two-dimensional system of strongly interacting electrons. At particular magnetic fields, the electron gas condenses into a remakable state with liquid-like properties. This state is very delicate, requiring high quality material with a low carrier concentration, and extremely low temperatures. As in the integer Quantum Hall Effect, a series of plateaux forms in the Hall resistance. Each particular values of magnetic field corresponds to a filling factor (the ratio of electrons to magnetic flux quanta) nu=p/q, where p and q are integers with no common factors). q always turns out to be an odd number. The principal series of such fractions are 1/3, 2/5, 3/7 etc, and 2/3, 3/5, 4/7, etc.
Figure 5: Fractional quantum Hall effect.
There are two main theories of the FQHE:
- Fractionally-charged quasiparticles. This theory, proposed by Laughlin, hides the interactions by constructing a set of quasiparticles with charge e*=e/q, where the fraction is p/qas above.
- Composite Fermions. This theory was proposed by Jain, and Halperin, Lee and Read. In order to hide the interactions, it attaches two (or, in general, an even number) flux quanta h/e to each electron, forming integer-charged quasiparticles called Composite Fermions. The fractional states are mapped to the Integer QHE. This makes electrons at a filling factor 1/3, for example, behave in the same way as at filing factor 1. A remarkable result is that filling factor 1/2 corresponds to zero magnetic field. Experiments support this.
The importance of the FQHE was recognised in 1998 by the award of the Nobel Prize for Physics to Tsui, Stormer and Laughlin, see this Nobel prize web site for more information.
Some of our research on the FQHE:
One-dimensional Electron Transport
Introductory article on low-dimensional systems published in Physics World in 2002.
By using a split-gate, it is possible to define a one-dimensional (1D) channel in the two-dimensional electron gas, as shown in the left inset. The channel width can be varied continuously by changing the applied gate voltage Vg on the split-gate.
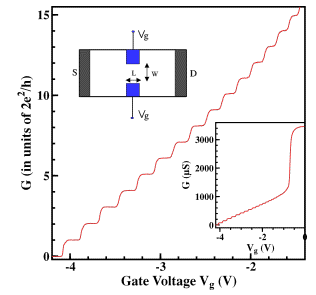Figure 6: 1D channel conductance.
If the mean free path is larger than the channel length L, and width w, one can observe ballistic 1D conductance plateaus, as illustrated in the right inset. This arises from cancellation of 1D density states and the group velocity. By subtracting the series resistance arising from leads and contacts, the 1D conductance steps are quantised in units of 2e2/h, as shown in Figure 6.
Coulomb Blockade in a Quantum Dot
By using the split-gate techniques pioneered in the Semiconductor Physics Group, one can form tunnel barriers which isolate a puddle of electrons, often called a "dot", from the leads. To add one electron to the dot costs a "charging energy" e2/C. The total capacitance of a sub-micron-sized dot to the surrounding gates and leads can be very small, less than 1 fF (10-15 F), so this energy is greater than the thermal energy for temperatures of a few Kelvin or less. Thus at such temperatures, transport through the dot is determined by Coulomb charging. Smaller dots can give even higher temperatures of operation.
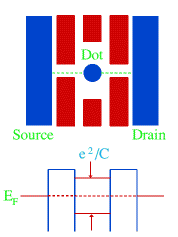Figure 7: Quantum dot.
For an electron to tunnel onto the dot, when the applied bias is small, there must be no net energy cost of adding an electron. Thus tunnelling can only occur when the size of the dot is such that it would be neutral if it contained an integer N plus a half electrons. Since it can only contain an integer number, the net charge on the dot will be ±e/2, depending on whether there are N or N+1 electrons in the dot. The charging energy is then (±e/2)2/C, which is the same in both cases. Hence changing the number of electrons in the dot between N and N+1 costs no energy, so electrons can flow on and off the dot with ease, and a current can flow. If the size of the dot is changed slightly, the charging energy in the two cases is no longer the same, and so the current falls to zero, only rising again when the size of the dot has changed by one electron. This is called the Coulomb Blockade (CB) of tunnelling. Sweeping a gate (shown in red in the figure) changes the size of the dot and thus the conductance between the leads (source and drain) has periodic peaks rising from zero to a value which may be as high as 2e2/h.
This effect can be seen in metal and semiconductor dots. In the latter, the quantum-mechanical energy levels of the electrons are also important, as their wavelength is comparable to the size of the dot, thus the term "quantum dot" is used. The number of electrons in a semiconductor dot can also sometimes be reduced all the way to zero, close to which the spacing of CB peaks becomes less regular as the energy spacing of the electronic states, and the mutual Coulomb interactions of the electrons in the dot, cannot be ignored.