Antidots
In a moderate or high magnetic field, electrons are confined to the edges of a sample, in edge states, one for each Landau level. We have developed techniques for fabricating a pair of constrictions on either side of a separately-contacted 0.3 micron diameter disc-shaped gate, giving complete control of each constriction using the gates.
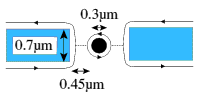 Figure 1: Diagram of an antidot.
Figure 1: Diagram of an antidot.The centre gate (when biased negatively) produces a hump in the potential (an "antidot"). Around the disc, an edge state comes back on itself, and interferes.
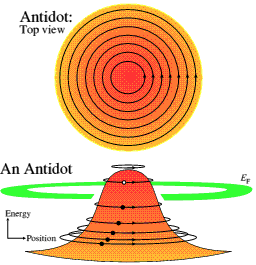 Figure 2: Edge states around an antidot.
Figure 2: Edge states around an antidot.In the constrictions, the edge states on either edge come close enough for there to be some tunnelling between them, giving rise to backscattering and hence increased resistance.
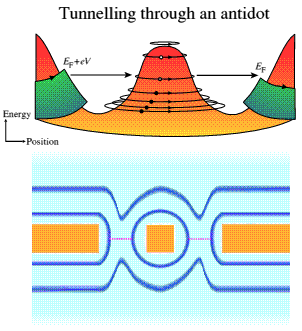 Figure 3: Tunnelling through an antidot.
Figure 3: Tunnelling through an antidot.The upper diagram in Figure 3 shows the potential and the states around the antidot, and the tunnelling from the edge states on the edges of the sample. The lower diagram is a schematic plan view of the antidot and side gates, with the edge states sketched in in blue around them, and a dotted line showing where the tunnelling occurs.
As the magnetic field or gate voltage is changed, the energy levels of the zero-dimensional states formed pass through the Fermi energy, causing the resistance to oscillate, through the Aharonov-Bohm effect, as shown in Figure 4.
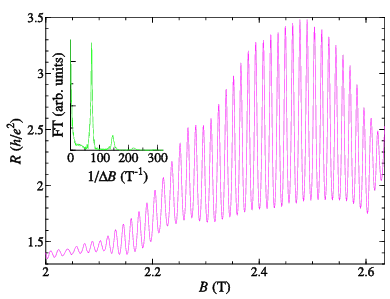 Figure 4: Aharonov-Bohm oscillations from an antidot.
Figure 4: Aharonov-Bohm oscillations from an antidot.Charging and Double-frequency Aharonov-Bohm Effects in an Open System
We have observed a number of surprising deviations from the usual Aharonov-Bohm oscillations with flux period h/e. The oscillations develop extra structure, such as double peaks. We can explain these effects in terms of transport through more than one of the edge states encircling the antidot. In conjunction with a computer model of scattering between the edge states, we have been able to determine the main types of scattering that may occur between edge states. However, not all our data may be explained in this way. Under some circumstances the oscillations double in frequency, indicating that two edge states are taking part. If the two states were independent, there would just be two sets of h/e oscillations with a phase difference between them that varied with magnetic field. Since we see no such change, we are forced to conclude that there is a Coulomb interaction between the two isolated edge states, as each may be able to charge up slightly before another electron can be added to the system (Ford et al. 1994, Simpson et al. 1994). This is the first demonstration of charging ("Coulomb blockade") in an open system. This is remarkable as, in an open system, electrons are constrained only by the magnetic field and the quantisation of the energy.
Similar devices have been made using holes instead of electrons, but no splitting of the oscillations was observed (Zailer et al. 1995). It is not yet known whether this difference is significant, or just caused by the difference in quality of the material.
The Fractional Quantum Hall Effect and Fractional Charge
At very high magnetic fields, Coulomb interactions between the electrons in the two-dimensional layer give rise to the Fractional Quantum Hall Effect (FQHE). At particular fields, the electron gas condenses into a remarkable system with liquid-like properties. This state is very delicate, requiring high quality material with a low carrier concentration, and extremely low temperatures. Despite the great theoretical interest in the effect, it is still poorly understood. Experiments show that edge states can exist as they do in the integer QHE. There is still no proof, however, that a generally-accepted explanation in terms of quasiparticles with a fractional charge is correct. Our separately-contacted disc gate is unique, and we have used the Aharonov-Bohm effect around it to investigate the FQHE, since the period of the oscillations as a function of magnetic field or disc size gives information about the quasiparticle's properties (Ford et al. 1994, Ford et al. 1995). For 1/3 filling factor around the antidot, Aharonov-Bohm oscillations are observed with the same magnetic field period as in the integer quantum Hall regime, as expected. We have also studied the temperature dependence and dc-bias behaviour to find the energy scales involved (Franklin et al. 1996). All our measurements are consistent with quasiparticles of fractional charge e*. However, we have been able to show with a simple theory that the results are also consistent with particles of any charge (>= e*) as the system must rearrange every time the flux enclosed increases by h/e. Thus an interpretation in terms of integer-charged particles (such as electrons or the recently-proposed composite fermions) is also possible. An important suggestion that we have confirmed is that, in the fractional regime, the system "relaxes" to a different lower energy state every time the flux increases by h/e, rather than charge building up along the edges until another electron can be fitted into the system. This breaks the Coulomb blockade which had been proposed for such antidot systems, although the two are equivalent in the quasiparticle picture.
