Low-dimensional electron systems in a perpendicular magnetic field
Low-field
The Hall voltage measured between probes on either side of a narrow current carrying channel in the presence of a perpendicular magnetic field B is approximately zero ("quenched") for a small range around B=0. This is due to electrons following fairly classical trajectories as they travel through the widened region at the junction between probes. The wave-like nature of electrons in such wires is demonstrated by splitting an electron wave into two and recombining it, using a ring-shaped wire with two leads attached. The partial waves interfere when they recombine, changing the resistance of the ring. To distinguish the interference from other effects, it can be made to vary periodically by applying a magnetic field perpendicular to the ring. Every time the flux through the ring changes by an amount h/e, an extra 2 pi of phase is added to the phase difference between the two waves, due to the Aharonov-Bohm effect. Thus the resistance oscillates with field. Changes of up to 50% of the resistance have been found.
Quenching of the Hall effect around zero magnetic field
The Hall voltage measured between probes on either side of a narrow current carrying channel in the presence of a perpendicular magnetic field B shows an anomaly around B=0. The Hall resistance fluctuates about zero (is "quenched"), before rising to a plateau at higher fields, and then rejoining the classical Hall line or forming quantised Hall plateaux (Roukes et al., 1987).
We confirmed the controversial measurements of Roukes et al. of this quenching of the Hall effect, (Ford et al., 1988). Our ability to vary the channel width was of great importance, since it showed that the quench developed gradually as the width was reduced. This observation confounded many subsequent theories and models proposed to explain the effect, and the most convincing model, put forward in 1989, produces this generic quenching by assuming a widening of the channel close to the junction with the probes, collimating the electrons entering the junction (Baranger and Stone, 1989).
Later, with Sean Washburn at the IBM T.J. Watson Research Center, Yorktown Heights, USA, we fabricated narrow Hall bars with junctions between current and voltage leads of various geometries. Widening the junction from the normal square-cornered shape produced a negative Hall resistance rather than a quench (Ford et al., 1989). With Markus Büttiker, we explained this with a classical trajectory in which the electrons entering the junction are bent around by the field towards a voltage probe, but they then hit the opposite, diagonal wall, and are reflected into the other ("wrong") voltage probe, making the Hall resistance negative. Adding an "island" in the centre of the junction deflects electrons more easily into the "correct" probe, giving rise to an enhanced Hall resistance instead. This supported the model of collimation proposed at that time by Baranger and Stone.
The Aharonov-Bohm effect
In 1957, Aharonov and Bohm predicted that if a quantum-mechanical wave-like particle were split into two partial waves, which then passed on either side of a region of magnetic field (eg a solenoid), then there would be a phase shift between the two waves. Thus, if they later recombined, the interference between them would depend on the amount of flux enclosed between the two waves. In fact, it is not the magnetic field B that actually matters, but the magnetic vector potential A. The wave/particle can even travel in a region where B is zero, provided that within the path there is some region containing magnetic flux! This seems strange, as A is not a well-defined quantity - there are many choices of A for a given B, depending on the "gauge" you choose. However, when the waves recombine, all that matters is the loop integral of A.dl, which is the same as the flux through the ring (by Stoke's Theorem).
The net result is that the phase accumulated is 2 pi for each h/e of flux enclosed within the two paths. This is the Aharonov-Bohm Effect. The same applies if a wave travels around a loop (being reflected or scattered at various points).
Our early work was aimed at demonstrating and investigating the Aharonov-Bohm (AB) effect in semiconductor rings. Even in high-quality heterostructures and at low temperatures, the phase-coherence length of electrons is only a few microns at most, and a ring must be of comparable circumference in order to show interference effects. To make rings, we used the recently-developed split-gate technique which allowed the width of the channels to be varied by changing the voltage on split gates on either side of the channels, in this case, around, and within, the ring. We used PMMA resist (a polymer used in lithography) as a spacer layer, to enable the gate in the central sub-micron region to be connected to that outside the ring, over the top of the resist.
We performed measurements on these rings at temperatures down to below 100 milliKelvin. The AB effect was clearly visible, changing the ring resistance by as much as 20%. Although AB oscillations in semiconductor rings were first observed at Bell Labs shortly before our measurements, we were able to vary the channel width to investigate the dependence of the AB oscillations on width, and found that the amplitude increased sharply with decreasing width, due in part to the reduced number of subbands occupied.
Later, with Alan Fowler at IBM Yorktown Heights, we tried to demonstrate an electrostatic method of changing the electrons' phase, like the Aharonov-Bohm effect. We made rings in which the two arms had different lengths, with a gate overall, to enable the carrier concentration, and hence the Fermi wavelength, to be varied, leading to a change in the phase due to the different path lengths. Aharonov-Bohm oscillations changing the resistance by up to 50% were found (Ford et al. 1990). Unfortunately, the results were not at all convincing, due to poor material and to potential fluctuations. They mainly showed that the probes at either end of the ring which were used to measure the resistance oscillations were still far enough away for the measurement to be effectively two-terminal. Such measurements must always give results that are symmetric in magnetic field.
High-field
In a high magnetic field, current-carrying electrons are confined to the edges of the sample by the Lorentz force, in edge states, one per Landau level. Many experiments in narrow structures are explicable in terms of Büttiker's theory that the Quantum Hall Effect is produced by edge states in both large and small structures (Büttiker 1986). For example, we found a series of dips ("resonances") along a quantum Hall plateau in a widened junction device. The dips take the Hall resistance right down to zero or even below (Ford et al 1991).
We can exclude electrons from a small island ("antidot") in the middle of a two-dimensional sea of electrons, so that they travel around the edge of the island. Because electrons are quantum-mechanical waves, they interfere with themselves when their paths close into loops, forming a set of states, or standing waves, around the island. Each state encloses one more unit of magnetic flux h/e than its neighbour, through the Aharonov-Bohm effect. We measure these states by making electrons tunnel through them between the other edges of the sample, so that the resistance depends on whether or not a state lines up with the Fermi level. This leads to a beautiful series of oscillations as the magnetic field is swept. We have used these oscillations to investigate the integer and fractional quantum Hall effects.
Quenching of the quantum Hall effect at high magnetic fields
At high magnetic fields of 1 to 3 Tesla, quantum Hall plateaux in our narrow Hall bars with widened junctions developed deep dips as the channels were narrowed (Ford et al., 1991). These were optimised by including constrictions at the entrances to the probes leading to the widened junction. This allows the probes to be made very narrow, confining edge states unambiguously to certain regions such as the junction itself. Along certain plateaux, dips ("resonances") which go down to zero are seen (Ford et al., 1991). George Kirczenow at Simon Fraser University in Canada constructed a model of the sample, obtaining similar dips (Kirczenow and Castano, 1991). The model assumes scattering between edge states at corners, giving an Aharonov-Bohm effect in the area enclosed between two edge states flowing along the same edge, in the region between two probes.
Edge states in the integer and fractional quantum Hall effects
In a moderate or high magnetic field, electrons are confined to the edges of a sample, in edge states, one for each Landau level in the Integer Quantum Hall Effect (IQHE). In the Fractional Quantum Hall Effect (FQHE), fractional edge states form, and their form is still very uncertain. We have developed a technique for changing the slope of the potential at an edge. This controls how independent the various edge states are, and the degree of scattering between them. A non-equilibrium occupation of the edge states is set up at one "end" of the edge, and the various edge states are measured 5-14 µm "downstream". This enables us to determine how much of the current has been transferred between edge states by scattering, and hence to learn about which edge states exist for a given slope. For example, a very steep edge has very few distinct edge states, so there is complete equilibration of the edge states, whereas we find distinct 1/5, 1/3 and 2/5 states for a very shallow potential.
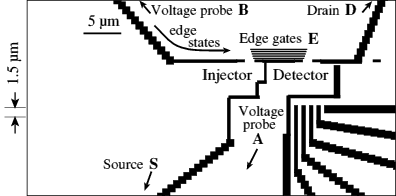

Details of some of this work are in Physica B 249-251, 405-409 (1998), as the Proceedings of EP2DS-12 (1997) (Franklin J.D.F., Ford C.J.B., Simmons M.Y., Ritchie D.A., and M. Pepper, "Non-equilibrium transport along an edge of variable slope in the fractional quantum Hall regime").
References
Baranger H U and Stone A D, 1989, Phys. Rev. Lett. 63, 414.
Büttiker M, 1986, Phys. Rev. Lett. 57, 1761.
Davies J H and Nixon J A, 1989, Phys. Rev. B 39, 3423.
Ford C J B, Washburn S, Bü ttiker M, Knoedler C M and Hong J M, 1989, Phys. Rev. Lett. 62, 2724.
Ford C J B, Fowler A B, Hong J M, Knoedler C M, Laux S E, Wainer J J, and Washburn S., 1990, Surf. Sci. 229, 307.
Ford C J B, Washburn S, Newbury R, Knoedler C M and Hong J M, 1991, Phys. Rev. B43, 7338.
Kirczenow and Castano, 1991, Phys. Rev. B43, 7347.
Roukes M L, Scherer A, Allen S J, Craighead H G, Ruthen R M, Beebe E D, and Harbison J P, 1987, Phys. Rev. Lett. 59, 3011.
