Spin-charge separation in quantum wires
The electron is a fundamental building block of nature and is indivisible in isolation, yet we have performed an experiment that shows that electrons in narrow wires can appear to split apart. The experiment was performed in the University of Cambridge's Cavendish Laboratory with the theoretical support coming from University of Birmingham physicists.
Electrons carrying a current through a wire are all negatively charged and so they repel each other as they move through the background of positive charge from the atoms in the lattice that gave rise to them. It is perhaps better to imagine them as forming a grid of points, all joined by springs to their neighbours. Give energy to one by moving it slightly, and it pulls all the surrounding electrons out of place, spreading the energy out almost instantly over all the particles. To excite the electrons in a way that does not dissipate energy like this, one can imagine moving a row or plane of electrons together. The energy still spreads out, but only at right angles to this row or plane. Now move each row by an amount that increases and decreases over the space of many rows, as in a wave, with no start or end. This wave can travel throughout the grid without losing energy. Waves of different wavelengths have different energies, and using quantum mechanics we can think of these waves as if they represent individual electrons, with the usual charge, but a different mass, so that they accelerate more quickly than individual free electrons when a force is applied. Crucially, the interactions between particles can largely be ignored.
Armed with this description of "quasi-electrons" forming a "Fermi liquid", one can explain nearly everything that happens in a metal or semiconductor, such as in the transistors in a computer chip or mobile phone. However, in some materials, at low temperatures or high magnetic fields, the approximation that interactions are unimportant breaks down and totally different behaviour is seen, such as superconductivity or the fractional quantum Hall effect. Even a very simple conducting system, a wire in which electrons can only move along the wire, so that it is one-dimensional, is not a Fermi liquid. To model the behaviour requires calculating forces between vast numbers of particles, which can never be carried out without some gross simplifications. In the one-dimensional wire, however, one straightforward approximation is enough to make the calculation exact. This system is called a Tomonaga-Luttinger (TL) liquid, after the first people to try this approximation. The calculation makes a very surprising prediction: that there are two ways in which a wave (like those travelling along the array of springs described above) can be excited at a given energy. One wave corresponds to the charge of the electron moving along the wire. The other is related to another property of electrons - their "spin", which gives rise, for example, to magnetism and may one day form the basis for a new type of electronics dubbed spintronics. Spin and charge waves are expected to travel at different speeds.
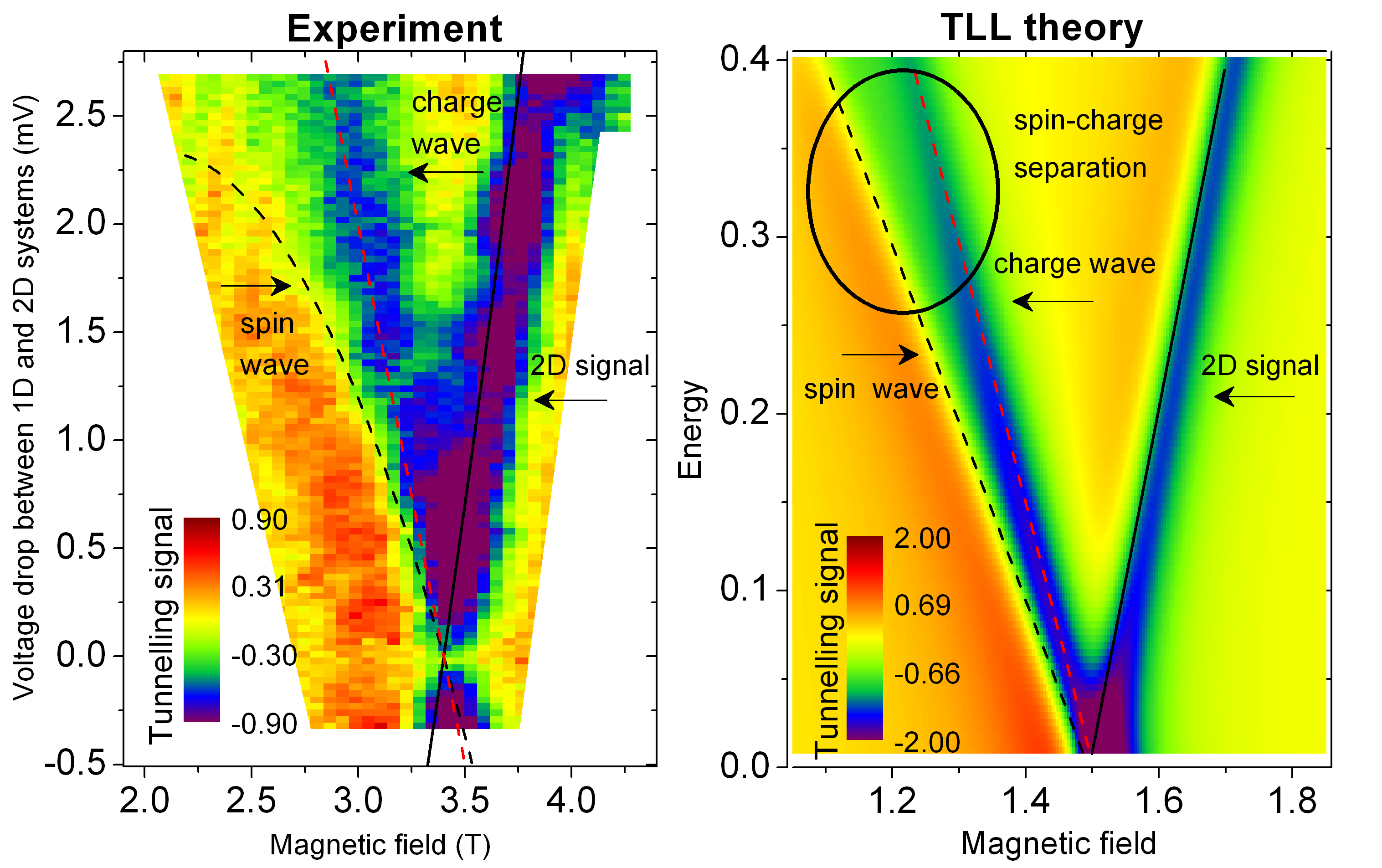 Figure 1: Lines corresponding to charge and spin waves (holons and spinons), for experiment and theory. The different slopes for each show that they travel at different speeds. The spin line is curved in experiment but not in theory, because of the approximation in the theory that makes the calculation possible.
Figure 1: Lines corresponding to charge and spin waves (holons and spinons), for experiment and theory. The different slopes for each show that they travel at different speeds. The spin line is curved in experiment but not in theory, because of the approximation in the theory that makes the calculation possible.How can this prediction be tested? If a wire is placed very close to another wire or plane, quantum mechanics allows electrons to "tunnel" from one to the other. Energy and momentum must be conserved, so the amount of current that flows between the two depends on the energies and speeds of the waves in the two systems. Applying a magnetic field gives electrons extra momentum as they tunnel, and a voltage between the two systems gives them extra energy. Thus one system can be used to map out the "excitations" of the other. In the past, tunnelling was measured between two 1D wires, giving an indication of the different speeds of spin and charge excitations. This used a 1D system to probe another identical system, requiring one to assume that all the details of the Tomonaga-Luttinger model were correct. Instead, Yodchay Jompol, Christopher Ford and colleagues in the Semiconductor Physics group at the Cavendish Laboratory of the University of Cambridge, supported by theorists Tim Silk and Andy Schofield at the University of Birmingham, have now used a two-dimensional layer of electrons as a well-understood, simpler, system to probe the 1D wire. Their results show two clear lines on a plot of the current as a function of magnetic field and voltage, corresponding to the different speeds of the spin and charge waves (see Figure 1). The extra line extends to higher energies than can be calculated using the simple TL approximation, providing an important test of more complicated theories yet to come.
1D wires are widely used to connect up quantum "dots", which may in the future form the basis of a new type of computer, called a quantum computer. Thus understanding their properties may be important for such quantum technologies, as well as helping to develop more complete theories of superconductivity and conduction in solids in general.
This research is published in Science 325, 597-601 (2009). Free download: Abstract, Download PDF, Full Text. Featured in This week in Science.
Beyond the Luttinger liquid
Having shown that 1D electrons interact strongly at low excitation energies, exhibiting the spin--charge separation predicted for a Luttinger liquid, we have now developed our device designs and fabrication techniques to allow detailed comparison with new theoretical advances, which predict extra curves (replicas of the usual dispersion relation for 1D wires in the absence of interactions) in plots of energy vs momentum. The theorists in our team (O. Tsyplyatyev and A. J. Schofield) have calculated that the magnitude of these replicas should increase strongly as the wire length is decreased, and indeed, in the shorter wires measured, we observe the start of the strongest replica. This is a completely new observation and it will give a boost to both experimental and theoretical work on interacting 1D systems in this new regime. In addition, the theory predicts a power-law dependence on energy, and we are accumulating evidence to test this.
As a spin-off of this work, we have developed a method for reliably fabricating large numbers of "air bridges" that join metal features on our devices, and this may be useful in making other types of research devices.
This work has been published in Phys. Rev. Lett., 114, 196401 (2015) and Phys. Rev. B, 93, 075147 (2016).
Press coverage:
